| A. Koutsioubas and A. G. Vanakaras, Langmuir, 24 (23), 13717–13722 (2008). DOI: 10.1021/la802536v |
|
Abstract: Structural properties of polymer brushes tethered on a periodically nanopatterned substrate are investigated by computer simulations. The substrate consists of an alternating succession of two different types of equal-width parallel 
stripes, and the polymers are end-tethered selectively on every second stripe. Three distinct morphologies of the nanopatterned brush have been identified, and their range of stability has been determined in terms of a single universal parameter that combines the grafting density, the polymer length, and the stripe width. We propose scaling relations for the average brush height and for the architectural properties of the outer surface of the nanopatterned brush under good solvent conditions. Our analysis provides guidelines for fabricating well-defined and tunable nanopatterned polymeric films. Copyright © 2008 American Chemical Society
S. D. Peroukidis, A. G. Vanakaras and D. J. Photinos, J. Mat. Chem., 20, 10495-10502, (2010).
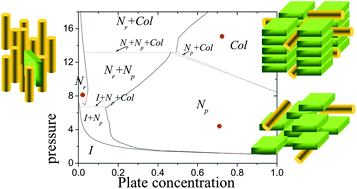Abstract. A theoretical model of shape-anisometric particles embedded in a cubic lattice is formulated for binary mixtures combining rod-like, plate-like and spherical particles. The model aims at providing a tool for the prediction and interpretation of complex phase behavior in a variety of liquid crystalline colloids, biological and macromolecular systems. Introducing just repulsive interactions among the particles, a rich variety of phase structures and multiphasic equilibria is obtained, including isotropic, nematic, lamellar and columnar phases, demixing into phases of the same or different symmetries and structural microsegregation of the different species of the mixture within the same phase.
This article is part of the collection: Modelling of Materials (c) http://pubs.rsc.org | doi:10.1039/C0JM01692F
S. Droulias, A.G. Vanakaras, D.J. Photinos, Liquid Crystals, 37:6, 969-976, (2010).
Abstract: A theory of thermotropic nematic liquid crystals in which molecules form internally ordered clusters is presented. The formulation is based on the same m
ean field approximation and form of the anisotropic potential used in the Maier-Saupe theory. A uniaxial nematic and two macroscopically isotropic phases are predicted. One of the isotropic phases consists of thermodynamically stable clusters with internal orientational order. The nematic phase shows cybotactic order throughout its range of stability. This order persists above the transition temperature, either as a stable feature or as a pretransitional effect. The values of the order parameter and of the entropy change at the nematic to isotropic phase transition depend on the size of the clusters. The Maier-Saupe theory is obtained in the limit of extremely large or extremely small clusters. URL: http://dx.doi.org/10.1080/02678292.2010.488819
G.A. Tritsaris and A.G. Vanakaras,
; DOI: 10.1021/la904613j.
Abstract: We demonstrate by computer experiments that the spontaneous formation of two-dimensional regularly patterned molecular networks containing voids may be an entirely entropy-driven process. On the basis of a simple model of core−(soft) shell half-disk-shaped particles, we show that, even without the mediation of any attractive interparticle forces, such particles self-organize to stable and macroscopically ordered patterns with regularly distributed voids. The morphology of these supramolecular porous motifs depends critically on the size of the core relative to the coronal halo. The reverse engineering analysis of these precise two-dimensional supramolecular porous templates suggests molecular-shape complementarity and polyphilicity as key design parameters for the bottom-up engineering of such functional substrates.
, and .
P.K. Karahaliou, A.G. Vanakaras and D.J. Photinos, J. Chem. Phys., 131, 124516 (2009).
Abstract: The possible symmetries of the biaxial nematic phase are examined against the implications of the presently available experimental results. Contrary to the widespread notion that biaxial nematics have orthorhombic symmetry, our study shows that a monoclinic $$C_{2h}$$ symmetry is more likely to be the case for the recently observed phase biaxiality in thermotropic bent-core and calamitc tetrapode nematic systems. The methodology for differentiating between the possible symmetries of the biaxial nematic phase by NMR and by IR spectroscopy measurements is presented in detail. The manifestations of the different symmetries on the alignment of the biaxial phase are identified and their implications on the measurement and quantification of biaxiality as well as on the potential use of biaxial nematic liquid crystals in electro-optic applications are discussed. ©2009 American Institute of Physics
S.D. Peroukidis, P.K. Karahaliou, A.G. Vanakaras and D.J. Photinos, Liq. Cryst., 36(6), 727-737 (2009).
Abstract: We studied the symmetry and spatial uniformity of the orientational order of the biaxial nematic phase in the light of recent experimental observations of phase biaxiality in thermotropic bent-core and calamitic-tetramer nematics. Evidence is presented supporting monoclinic symmetry, instead of the usually assumed orthorhombic symmetry. The use of deuterium nuclear magnetic resonance to differentiate between the possible symmetries is described. The spatial aspects of biaxial order are presented in the context of the cluster model, wherein macroscopic biaxiality can result from the field-induced alignment of biaxial and possibly polar domains. The implications of different symmetries on the alignment of biaxial nematics and on the measurements of biaxial order are discussed in conjunction with the microdomain structure of the biaxial phase.
A.G. Vanakaras and D.J. Photinos, J. Chem. Phys., 128, 154512 (2008).
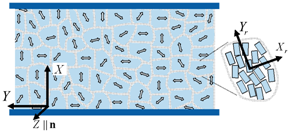Abstract: An intermediate nematic phase is proposed for the interpretation of recent experimental results on phase biaxiality in bent-core nematic liquid crystals. The phase is macroscopically uniaxial but has microscopic biaxial, and possibly polar, domains. Under the action of an electric field, the phase acquires macroscopic biaxial ordering resulting from the collective alignment of the domains. A phenomenological theory is developed for the molecular order in this phase and for its transitions to purely uniaxial and to spontaneously biaxial nematic phases.
Related Works:
- Theory and simulation of biaxial nematic and orthogonal smectic phases formed by mixtures of board-like molecules, A. G. Vanakaras, M. A. Bates and D. J. Photinos, Phys. Chem. Chem. Phys. 5(17), 3700 (2003).
- The phase behavior of a binary mixture of rodlike and disclike mesogens: Monte Carlo simulation, theory, and experiment, A. Galindo, A. J. Haslam, S. Varga, G. Jackson, A. G. Vanakaras, D. J. Photinos and D. A. Dunmur, J. Chem. Phys. 119(10), 5216 (2003).
- On the Molecular requirements for the stabilization of thermotropic Biaxial ordering in Rod-Plate nematics, A. G. Vanakaras, A. F. Terzis and D.J. Photinos, Molec.Cryst. Liq. Cryst., 362, 67-78 (2001).
- Theory of biaxial nematic ordering in rod-disc mixtures revisited, A. G. Vanakaras and D.J. Photinos, Molec.Cryst. Liq. Cryst., 299, 65-71 (1997).
- Hydrogen bonding and phase biaxiality in nematic rod-plate mixtures, A. G. Vanakaras, S. C. McGrother, G. Jackson and D. J. Photinos, Molec.Cryst. Liq. Cryst., 323, 199 (1998).
http://www.matersci.upatras.gr/SoftMat/Research/PDF/JCP08_BiaxClusters.pdf
S.D. Peroukidis, A.G. Vanakaras and D.J. Photinos, J. Phys. Chem. B , 112(40), 12761-12767 (2008).
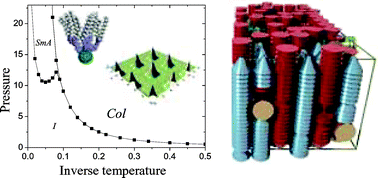Abstract: The molecular cubic-block model [J. Chem. Phys. 2005, 123, 164904] is used to study a class of poly(benzyl ether) fullerodendrimers that have recently been reported to form columnar liquid crystal phases. In agreement with experiment, the model-molecules are found to self-assemble into columns which form hexagonal or rectangular lattices. The columnar cross sections are elongated in the rectangular phase. Transitions to the isotropic phase, either directly or through the intermediate formation of smectic phases, have been found. The effects of dissolving small amounts of nonbonded fullerene molecules have been explored. The results predict that the fullerene solutes restrict the range of stability of the columnar phase and may induce transitions from the columnar to the smectic or the isotropic phase. ©2008 American Chemical Society
Related Works:
, S. D. Peroukidis, A. G. Vanakaras and D. J. Photinos,
J. Chem. Phys.,
123, 164904 (2005).
, S. D. Peroukidis , A. G. Vanakaras and D. J. Photinos,
Soft Matter,
4, 493-499 (2008).
A. G. Vanakaras and D. J. Photinos,
J. Mater. Chem. 15, 2002-2012 (2005).
S.D. Peroukidis, A.G. Vanakaras and D. J. Photinos, Soft Matter, 4, 493-499 (2008).
Abstract: A molecular model of cubic building blocks is used to describe the mesomorphism of conical fullerenomesogens. Calculations based on density functional molecular theory and on Monte Carlo computer simulations give qualitatively similar results that are also in good agreement with the experimentally observed mesomorphic behaviour. The columnar and lamellar mesophases obtained are non-polar, and their relative stability is controlled by a single model parameter representing the softness of the repulsive interactions among the building blocks of the conical molecules.
D. K. Christopoulos, A. F. Terzis, A. G. Vanakaras and D. J. Photinos, J. Chem. Phys., 125, 204907 (2006).
Abstract: We present a molecular simulation study of the structure of linear dendronized polymers. We use excluded volume interactions in the context of a generic coarse grained molecular model whose geometrical parameters are tuned to represent a poly(paraphenylene) backbone with benzyl ether, Frechet-type dendrons. We apply Monte Carlo sampling in order to investigate the formation of packing-induced chiral structures along the polymer backbone of these chemically achiral systems. We find that helical structures can be formed, usually with defects consisting of domains with reversed helical handedness. Clear signs of helical arrangements of the dendrons begin to appear for dendritic generation g=4, while for g=5 these arrangements dominate and perfect helices can be observed as equilibrium structures obtained from certain types of starting configurations.
